What is Teradata Statistics Extrapolation?
A quite usual scenario in data warehousing is the daily population of snapshot historized tables, with data valid for the most recent date.
Here is a typical example:
SELECT Snapshot_Date,Count(*) CNT FROM The_Snapshot_Table;
| Snapshot Date | CNT |
| 2015-04-10 | 10 |
| 2015-04-11 | 15 |
| 2015-04-12 | 10 |
| 2015-04-13 | 25 |
| 2015-04-14 | 15 |
| 2015-04-15 | 30 |
— We assume in our example, that statistics are collected on 2015-05-15, after the daily snapshot for 2015-01-15 was loaded:
COLLECT STATISTICS ON THE_SNAPSHOT_TABLE COLUMN(SNAPSHOT_DATE);
After loading 2015-04-16, and without extrapolation, for queries accessing snapshot date 2015-04-16, the optimizer would expect zero rows to be returned (assuming statistics are not recollected). For example, the optimizer would expect 0 rows to be returned in the query below:
SELECT * FROM The_Snapshot_Table WHERE Snapshot_Date=DATE'2015-04-16′
Which is Statistics Information extrapolated?
The optimizer is extrapolating the following statistical information:
- The number of table rows, based on the available statistics summary information and random-AMP sampling
- The number of distinct primary index values and the maximum value per statistic histogram
- The number of rows per value for the date column
How is the Statistics Information extrapolated?
It is important to understand that the optimizer only estimates a certain number of dates into the future (future in this context means any date after the last date for which collected statistics exist). The highest estimated date used for extrapolation is based on a random AMP sample. In the extrapolation process, the random AMP sample gives information about the number of distinct future dates.
Below extrapolation formula is used to calculate the highest future date:
Here is an example with 1000 Average Rows per Date from Collected Statistics, the random AMP sample is assumed to return 10 different future dates:
Maximum Extrapolated Date = 2015-03-30 + ((2015-03-30 – 2015-01-01) * ((10 * 1000) / (89 * 1000)) = 2015-04-09
Assuming that our query selects a date range between 2015-03-25 and 2015-04-09, the estimated number of rows will be:
Estimated Rows from Collected Stats + Estimated Rows from Extrapolation: (6*1000) + (10*1000) = 16000 Rows.
As we can see, the estimation is much better than without extrapolation (the optimizer would only have estimated 6000 rows from the collected, but stale statistics).
The quality of the estimation based on a random AMP sample highly depends on the skew factor of the table.
The excellent case is when the random AMP sampling delivers all distinct future dates, but a skewed table may result in an entirely wrong estimation of different future dates.
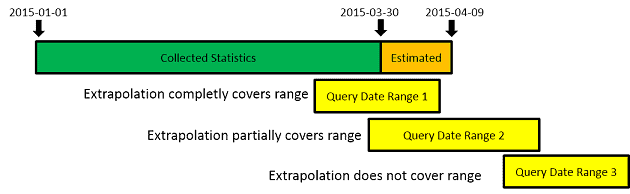
Another important influence factor is how the extrapolated dates are covering the date range of your query.
The optimal situation is if the collected statistics plus the extrapolated statistics include the query date range entirely. Even if only a part of the extrapolated statistics includes your query, the overall estimated statistics will be better than without statistics extrapolation.
Only in the case that your query date range is not covered by the extrapolated statistics at all, there is no advantage from extrapolation
Although statistics extrapolation can be very helpful in the case of snapshot tables which are loaded on a daily base, this should not be an excuse to stop collecting statistics all. Extrapolation helps you to move your recollection process to a point in time when your Teradata system is less loaded.
You are right regarding point (1) and I always wondered why this may be the reason? My assumption was that during the process it’s easier as “division by zero” handling can be avoided?
Regarding point (2), as far as I remember, the calculation formula is available in the official documentation.
Hi Roland,
Interesting article, thanks. I have a couple of points/questions:
1) (minor point), AFAIK the optimizer never estimates ‘0 rows’, the minimum value it uses is 1 row or ‘1 row per amp’.
2) (question) where did you get the extrapolation calculation from?
Cheers,
Dave