To comprehend the issue of Teradata hash collisions, I will briefly explain how rows are allocated. If you are unfamiliar with Teradata Architecture or require a refresher, I suggest reading the following article beforehand:
As you know, a hashing algorithm distributes a table’s rows to the AMPs.
The Foundations
The hashing algorithm accepts one or multiple column values as input and outputs a 32-bit integer known as ROWHASH.
Two crucial attributes of this hashing function are vital when discussing hash collisions:
- The same input values always produce the same ROWHASH
- Different input values can generate the same ROWHASH
The second feature piques our interest is the ROWHASH, a 32-bit integer. As previously stated.
Over 4 billion unique ROWHASH values can be created, resulting in the possibility of hash collisions occurring after every 4 billion rows.
Teradata hash collisions are why it is insufficient to know the ROWHASH to locate a row in a data block.
Therefore, every time a row is searched, the ROWHASH and the searched value must be passed to the AMP in the parsing engine’s message.
In addition, a 32-bit integer is appended to the Rowhash, which uniquely identifies the row. This 32-bit integer, together with the ROWHASH, is called ROWID.
The first 16 or 20 bits (depending on the Teradata System) of the ROWHASH are the so-called Hash Bucket. The hash bucket determines which entry in the hash map is responsible for this row. Finally, the hash map shows the target amp.
A Case Study On Teradata Hash Collisions
It is important to exercise caution when character columns are designated as the primary index, despite the effectiveness of the Teradata Hashing Algorithm in ensuring proper distribution and preventing hash collisions. Consider the following example.
We first create two tables. The primary index of one table is of data type BIGINT. The second table has a primary index of data type VARCHAR(30):
CREATE TABLE DWHPRO.COLLISION_YES
(
PK VARCHAR(30) NOT NULL
) PRIMARY INDEX (PK);
CREATE TABLE DWHPRO.COLLISION_NO
(
PK BIGINT NOT NULL
) PRIMARY INDEX (PK);The two tables are populated four times with varying SAMPLE sizes of 40 million, 80 million, 120 million, and 160 million rows. Hash collisions are then checked after each load.
INSERT INTO DWHPRO.COLLISION_NO
SELECT ROW_NUMBER() OVER (ORDER BY 1) FROM DWHPRO.A_HUGE_TABLE
SAMPLE <n>;
INSERT INTO DWHPRO.COLLISION_YES
SELECT TRIM(ROW_NUMBER() OVER (ORDER BY 1)) FROM DWHPRO.A_HUGE_TABLE
SAMPLE <n>;SELECT COUNT(*) FROM
(
SELECT HASHROW(PK) AS HashValue ,COUNT(*) X FROM DWHPRO.COLLISION_NO
GROUP BY 1 HAVING X > 1
) X;
SELECT COUNT(*) FROM
(
SELECT HASHROW(PK) AS HashValue ,COUNT(*) X FROM DWHPRO.COLLISION_YES
GROUP BY 1 HAVING X > 1
) XThis is the query result:
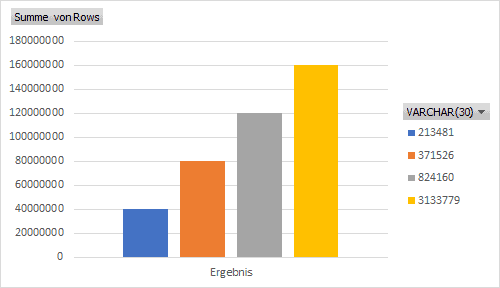
| Rows | BIGINT | VARCHAR(30) |
| 40 Mio | 0 | 213481 |
| 80 Mio | 0 | 371526 |
| 120 Mio | 0 | 824160 |
| 160 Mio | 0 | 3133779 |
The hashing function is more stable when using integer data types. BIGINT has no Teradata hash collisions at any sample size.
The case is desperate for a VARCHAR(30) primary index:
Conclusions
With a table containing 120 million rows, the occurrence of one hash collision per 4 billion rows is not as expected. In fact, in this example, the number of collisions exceeds 3 million.
Teradata hash collisions waste valuable CPU time, complicating searching for data and storing rows in data blocks. While this may not initially be a concern for a few collisions, the impact on CPU performance will eventually become evident.
It is important to consider the design of your Primary Index carefully. Utilizing surrogate keys in your data warehouse can be a beneficial approach.

